leetcode5.1-5.7
5.1
哈希表
383.赎金信
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
unordered_map<int,int> m;
for(int i=0;i<magazine.size();i++){
m[magazine[i]]++;
}
for(int i=0;i<ransomNote.size();i++){
m[ransomNote[i]]--;
if(m[ransomNote[i]]<0){
return false;
}
}
return true;
}
};
|
今天出去吃了顿夜宵,晚上刷力扣时间耽搁了,明天补
5.2
哈希表
15.三数之和
对于哈希表的应用还是没有头绪,这道题开始也没有想到哈希表的常规作法,然而看了题解才知道哈希表面临去重的问题,对结果向量进行去重会超时,后面这道题还是用了双指针的方法。
- 首先要对数组进行排序(这个很关键)
- 然后从i=0开始遍历,对num[i]进行去重,i=1开始,如果相同就跳过这轮循环
- 在这轮循环内,分别设置left=i+1,right=num.length()-1;这是另外两个数的索引,left和right这个区间不断缩小去寻找符合条件的值,同时也要去重,去重是向区间里去重。
- 然后进入新的循环,重新寻找符合条件的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();i++){
if(nums[i]>0)
return res;
if(i>0&&nums[i]==nums[i-1])
continue;
int left=i+1,right=nums.size()-1;
while(left<right){
if(nums[i]+nums[left]+nums[right]>0){
right--;
}
else if(nums[i]+nums[left]+nums[right]<0){
left++;
}
else
{
res.push_back(vector<int>{nums[i],nums[left],nums[right]});
while(left<right&&nums[right]==nums[right-1]) right--;
while(left<right&&nums[left]==nums[left+1]) left++;
right--;
left++;
}
}
}
return res;
}
};
|
tip1:
说道去重,其实主要考虑三个数的去重。 a, b ,c, 对应的就是 nums[i],nums[left],nums[right]
a 如果重复了怎么办,a是nums里遍历的元素,那么应该直接跳过去。
但这里有一个问题,是判断 nums[i] 与 nums[i + 1]是否相同,还是判断 nums[i] 与 nums[i-1] 是否相同。
有同学可能想,这不都一样吗。
其实不一样!
都是和 nums[i]进行比较,是比较它的前一个,还是比较他的后一个。
如果我们的写法是 这样:
1
2
3
| >if (nums[i] == nums[i + 1]) {
continue;
>}
|
那就我们就把 三元组中出现重复元素的情况直接pass掉了。 例如{-1, -1 ,2} 这组数据,当遍历到第一个-1 的时候,判断 下一个也是-1,那这组数据就pass了。
我们要做的是 不能有重复的三元组,但三元组内的元素是可以重复的!
所以这里是有两个重复的维度。
那么应该这么写:
1
2
3
| >if (i > 0 && nums[i] == nums[i - 1]) {
continue;
>}
|
这么写就是当前使用 nums[i],我们判断前一位是不是一样的元素
不能有重复的三元组但是三元组内的元素可以重复
如果判断后一位是否和当前位相同,由于当前位还没有判断是否满足,可能会遗漏三元组中出现重复元素的情况;
但是如果判断前一位是否相同,由于前一位已经经过了判断,所以可以保证它只是排除了与前一轮放进答案相同的情况。
5.3
5.4(今天开始加上题目链接)
哈希表
对于15.三数之和 双指针法就是将原本暴力O(n^3^)的解法,降为O(n^2^)的解法,四数之和的双指针解法就是将原本暴力O(n^4^)的解法,降为O(n^3^)的解法。
- 在三数之和的基础上多了一重循环,最后两层循环由双指针法降为O(n)
- target不是固定的数,因此剪枝的逻辑需要改变,仅仅大于target不够,因为负数相加会更小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> res;
sort(nums.begin(),nums.end());
for(int k=0;k<nums.size();k++){
if(nums[k]>target&&nums[k]>0){
break;
}
if(k>0&&nums[k]==nums[k-1]){
continue;
}
for(int i=k+1;i<nums.size();i++){
if(nums[k]+nums[i]>target&&nums[k]+nums[i]>0){
break;
}
if(i>k+1&&nums[i]==nums[i-1]){
continue;
}
int left=i+1;
int right=nums.size()-1;
while(left<right){
if((long)nums[i]+nums[k]+nums[left]+nums[right]<target){
left++;
}
else if((long)nums[i]+nums[k]+nums[left]+nums[right]>target){
right--;
}
else{
res.push_back(vector<int>{nums[i],nums[k],nums[left],nums[right]});
while(left<right&&nums[left]==nums[left+1]) {
left++;
}
while(left<right&&(nums[right]==nums[right-1])){
right--;
}
left++;
right--;
}
}
}
}
return res;
}
};
|
5.5
今天偷懒了,二叉树的前中后遍历,三道easy
买一送二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
midtravel(root,result);
return result;
}
void midtravel(TreeNode* root,vector<int>& res){
if (!root) return;
midtravel(root->left,res);
res.push_back(root->val);
midtravel(root->right,res);
}
};
|
5.6
递归反转链表
其实主要是用递归的方法去反转链表的基本思路,写出反转一个链表的递归方法后再逐步优化到选择指定的节点区域反转。
递归的处理重点是不要跳进递归,用明确的定义来实现算法逻辑
1
2
3
4
5
6
7
8
9
| ListNode* reverse(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
ListNode* last = reverse(head->next);
head->next->next = head;
head->next = nullptr;
return last;
}
|
输入一个节点 head,将「以 head 为起点」的链表反转,并返回反转之后的头结点。
不用管reverse(head->next) 里面会怎么样,只要知道这一步返回了剩余部分的反转后的头结点
如图:

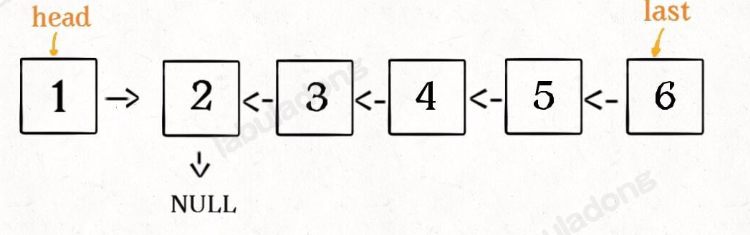
所以,剩下的就是将head->next 即 2的next 指向1,1的next指向null
2.在此基础上实现反转前N个节点
区别:
1、base case 变为 n == 1,反转一个元素,就是它本身,同时要记录后驱节点。
2、刚才我们直接把 head.next 设置为 null,因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 successor(第 n + 1 个节点),反转之后将 head 连接上。
3.完成本题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
private: ListNode* success=nullptr;
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
if(left==1){
return reverseN(head,right);
}
head->next=reverseBetween(head->next,left-1,right-1);
return head;
}
ListNode* reverseN (ListNode* head,int n){
if(n==1){
success=head->next;
return head;
}
ListNode* last=reverseN(head->next,n-1);
head->next->next=head;
head->next=success;
return last;
}
};
|
要注意反转前N个的函数里success即N后面的节点位置要用全局变量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if(head==nullptr) return nullptr;;
ListNode* a,*b;
a=b=head;
for(int i=0;i<k;i++){
if(b==nullptr) return head;
b=b->next;
}
ListNode* newhead=reverse(a,b);
a->next=reverseKGroup(b,k);
return newhead;
}
ListNode* reverse(ListNode* a,ListNode* b){
ListNode* pre,*cur,*next;
pre=nullptr,cur=a,next=a;
while(cur!=b){
next=cur->next;
cur->next=pre;
pre=cur;
cur=next;
}
return pre;
}
};
|
5.7
二叉树
写递归感觉比以前稍微好那么一点了,还是很受昨天的这句话的启发,”递归的处理重点是不要跳进递归,用明确的定义来实现算法逻辑”。虽然还是很弱,能有一些好的变化还是很开心的。😀
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==nullptr) return root;
swap(root->left,root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}
};
|
传入root,返回值可以不用但是题目要求了
节点为空的时候返回
因为是先前序遍历,所以先进行交换左右孩子节点,然后反转左子树,反转右子树。

